Kaleidocycles are a mechanical toy featuring a number of tetrehedra chained together to form a loop which can be rotated in on itself. They were popularised and named by Wallace Walker in the 1950s; and have continued to show up in media and museum gift shops ever since.

I'm not 100% sure where I came across one at first, but I'm pretty sure it was simply a video online like this:

As usual I couldn't help myself but build one (origami instructions here); and once I began playing with it I immediately got to thinking about what the exact shape of these forms are, as well as what other shapes might work.

After some thought and a few days of play I ended up doing a bit of hand wavy geometry to calculate the geometry of regular kaleidocycles (see below). With this in mind I built an 8 sided & 10 sided kaleidocycle and felt awfully clever.

Of course eventually I started looking up some of the maths to see if anyone else had made further progress and I found a wonderful article which seems to no longer be officially online but is here, thanks to the wayback machine.

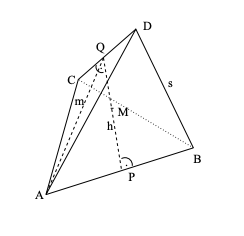They uncovered a whole suite of kaleidocycles which work based on maintaining the same geometry between the connected joints, but modifying the actual tetrahedron geometry. With this information in hand I decided I needed to code up a version for myself to play with (given I wasn't about to build hundreds more of these). The code I wrote can be found on my github, and played with below (modify offsets PA/PB/QC/QD to change the ratio of sides on the tetrehedons).

Deriving kaleidocycle side lengths

Let's begin with the six sided kaleidocycle.

The first step is to look at the kaleidocycle in it's closed position - when a set of points meets in the center (try setting the viewer above to any multiple of \(90^\circ\)).

A displays top down. B faces a single triangular face. Hinges are shown in red.

Given that the hinged edges are of length \(R\), and assuming noting that from this top down perspective the kaleidocycle is a perfect hexagon we can see that the edge length must also be \(R\).

Rotating to look directly at the face we can see that the top down edge length is actually the width of the triangle.

With this in mind we can calculate the long edges \(l\) to be exactly \(\sqrt{R^2 + (\frac{R}{2})^2} = \sqrt{5}\frac{R}{2}\)

More sided kaleidocycles

Given the above derivation it was only a few more steps to determine the geometry of an N sided kaleidocycle. Because it's a little bit cleaner we define hinge length of \(R = 2r\) and simply use \(r\) in future equations.

A. Given all corners meet perfectly in the middle of the closed kaleidocycle we can be certain that the internal corner (\(\theta_1\)) is exactly \(\theta_1 = 360^\circ/n\).

We know that once we rotate the kaleidocycle 180 degrees all of the outside points must now be inside points and must also be exactly \(\theta_2 = 360^\circ/n\); thus \(\theta_1 = \theta_2\).

B. Now we can calculate length \(w\) using simple trigonometry to be \( w = r/cos\theta\)

C. we know this is the width of the face of our tetrahedrons and can calculate our edge length \(l\) to be

With this knowledge we can calculate all the regular kaleidocycles!

Even more Kaleidocycles

Another thought I had had while looking into these was whether or not the connecting hinges must be at right angles to one another - I could not satisfactorily come up with an answer, but recently found an amazing paper by Johannes Schönke and Eliot Fried which explores and describe these "mobius kaleidocycles" in full!